Modellazione, Analisi e Verifica degli Edifici in Muratura

Ing. Alberto Pingitore - Ingegnere Strutturista

Abstract

Questo report fornisce una guida sintetica per la modellazione, l'analisi e la verifica degli edifici in muratura, con riferimenti alla normativa italiana (NTC 2018) e agli Eurocodici (EN 1996). Vengono descritti approcci di modellazione (telaio equivalente, macro-elementi, micro-modelli), metodi di analisi (lineare, dinamica, pushover) e criteri di verifica agli SLU e SLE. Il documento include le formule di calcolo principali, schemi illustrativi e un esempio numerico di modellazione di un edificio in muratura a due piani.

1. Introduzione e inquadramento normativo

Gli edifici in muratura costituiscono una porzione significativa del patrimonio edilizio nazionale, in particolare per l'edilizia storica e residenziale minore. La progettazione, la modellazione e la verifica strutturale di tali edifici devono fare riferimento alle Norme Tecniche per le Costruzioni (D.M. 17/01/2018 - NTC 2018) e alle relative circolari esplicative, nonché alle regole contenute nell'Eurocodice 6 (EN 1996-1-1) per gli aspetti di resistenza e durabilità. Il comportamento meccanico della muratura è intrinsecamente nonlineare: la risposta in compressione, la scarsa duttilità in taglio e la presenza di elementi discontinui (aperture, lesioni, connessioni deboli) rendono necessaria una modellazione attenta e, quando opportuno, calibrazione sperimentale.

Riferimenti normativi principali:

• NTC 2018;
• Circolare esplicativa NTC 2018;
• EN 1996-1-1 (Eurocode 6).

2. Modellazione strutturale

La modellazione della muratura può essere affrontata con diversi livelli di idealizzazione, a seconda degli obiettivi progettuali:

- Telaio equivalente: l'edificio è rappresentato tramite maschi verticali (pareti) e fasce orizzontali (solai), convertiti in elementi trave/colonna con rigidezze e resistenze equivalenti. Questo approccio è largamente usato per analisi pushover e per valutazioni sismiche preliminari;

- Macro-elementi: la muratura è discretizzata in elementi non-lineari che concentrano i meccanismi (ribaltamento, scorrimento) e catturano il comportamento ciclico; sono ideali per analisi non-lineari globali con un buon compromesso tra dettaglio e tempo di calcolo.

- Micro-modelli: modellano mattoni e malta separatamente (interfacce), spesso con elementi finiti e leggi costitutive complesse; utili per studi locali o per indagini su particolari costruttivi. La scelta del modello dipende dall'accuratezza richiesta: per una verifica sismica dettagliata di un edificio storico si preferiscono macro-elementi o micro-modelli; per analisi di screening il telaio equivalente è spesso sufficiente.

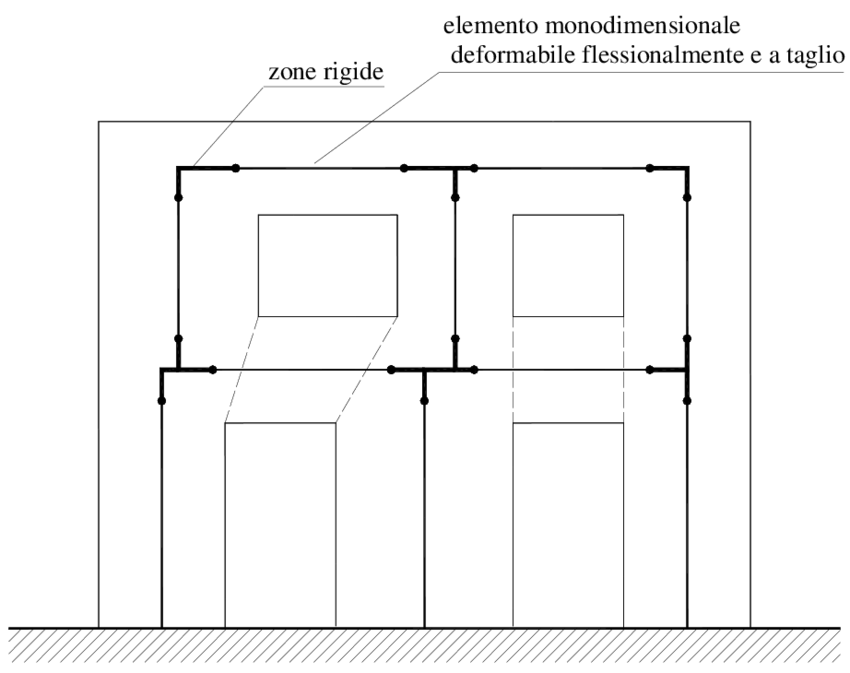
Figura 1 - Schema a telaio equivalente: maschi (verticali) e fasce (orizzontali).

3. Formule di calcolo principali e criteri di verifica

In questa sezione sono raccolte le formule più utilizzate per la progettazione e la verifica degli elementi in muratura.

Stress normale medio nel maschio: σ = N / A

Tensioni per pressoflessione: σ(x) = N / A ± M / W (dove W è il modulo di resistenza)

Verifica a compressione locale: σ ≤ fm (resistenza media della muratura)

Capacità di taglio di parete (semplificata): VR = τ0 x t x l (τ0 resistenza tangenziale media, t spessore, l altezza efficace)

Equilibrio domanda-capacità (pushover): Sd ≤ Sc (domanda ≤ capacità)

Esempio di calcolo: verifica pressoflessione di un maschio

Consideriamo un maschio murario rettangolare con le seguenti proprietà:

Altezza utile h = 3.0 m, spessore t = 0.30 m, larghezza b = 1.0 m (area A = 0.30 m²).

- Carico assiale N = 150 kN (compressivo).

- Momento flettente M = 10 kNm.

- Resistenza media della muratura f_m = 2.5 MPa (2500 kN/m²) (esempio tipico; la caratterizzazione sperimentale è necessaria per casi reali).

Calcoliamo lo sforzo medio e verifichiamo la condizione di sicurezza.

Area A = 0.300 m². Carico assiale N = 150.0 kN. Momento M = 10.0 kNm.

Sforzo medio σ = N/A = 0.500 MPa.

Modulo di resistenza approssimato W = b·t²/6 = 0.0150 m³.

Sforzo per flessione σM = M/W = 0.667 MPa.

Sforzi risultanti: estremità superiore σtop = 1.167 MPa; estremità inferiore σbottom = -0.167 MPa.

Confronto con resistenza media fm = 2.5 MPa: σtop ≤ fm; σbottom ≤ fm.

4. Analisi strutturale e valutazione sismica

Per la valutazione sismica sono frequentemente impiegati i seguenti approcci: analisi lineare dinamica (risposta spettrare), analisi non-lineare statica (pushover) e analisi non-lineare dinamica (time-history). L'analisi pushover consente di estrarre la curva di capacità (Forza risultante vs spostamento) e di determinare il punto di equilibrio con la domanda sismica. La rappresentazione grafica della curva di capacità e del punto di prestazione è utile per la valutazione immediata del margine di sicurezza.

Figura 2 - Curva pushover (capacitá) idealizzata.

5. Verifica e miglioramento

Le verifiche agli SLU si concentrano su meccanismi globali (collasso a pannelli, ribaltamento di pareti) e su meccanismi locali (lesioni concentrate, espulsione di angoli).

Interventi tipici di miglioramento comprendono catene in acciaio, intonaci armati, cordoli orizzontali/verticali, iniezioni di malta e rinforzi locali mediante compositi.

Conclusioni

L'analisi degli edifici in muratura richiede l'uso combinato di modelli appropriati, dati sperimentali per la caratterizzazione dei materiali e procedure di verifica coerenti con la normativa. Il modello a telaio equivalente resta un ottimo compromesso tra dettaglio e praticità per valutazioni sismiche preliminari, mentre macro- e micro-modelli sono raccomandati per analisi approfondite o per edifici di pregio storico.

Bibliografia

Decreto Ministeriale 17 gennaio 2018 - NTC 2018 (Norme Tecniche per le Costruzioni).

Circolare esplicativa NTC 2018 (Circolare 21 gennaio 2019, n.7).

EN 1996-1-1: Eurocode 6 - Design of masonry structures.

Lagomarsino S., Penna A., Galasco A., Cattari S. (2013). TREMURI program: An equivalent frame model for the nonlinear seismic analysis of masonry buildings. Engineering Structures.

Gambarotta L., Lagomarsino S. (1997). Damage models for the seismic response of brick masonry shear walls. Earthquake Engineering & Structural Dynamics.